1. 테니스를 좋아하는 모든 사원은 탁구를 좋아한다.
2. 테니스를 좋아하는 어떤 사원은 탁구를 좋아하지 않는다.
3. 탁구를 좋아하는 모든 사원은 테니스를 좋아한다.
4. 탁구를 좋아하는 어떤 사원은 테니스를 좋아한다.
5. 탁구를 좋아하지 않는 어떤 사원은 테니스를 좋아하지 않는다.
풀이 펼치기
우선 볼링 테니스 탁구 벤 다이어그램을 다음과 같이 그린다.
첫 번째 전제 : 볼링을 좋아하는 모든 사원은 테니스를 좋아한다.
따라서 아래의 벤 다이어그램의 X 부분은 존재할 수 없다.
1. 책이 있는 어떤 카페는 손님이 많다.
2. 책이 있는 모든 카페는 손님이 많지 않다.
3. 손님이 많은 어떤 카페는 책이 있다.
4. 손님이 많은 모든 카페는 책이 있다.
5. 손님이 많지 않은 모든 카페는 책이 없다.
풀이 펼치기
우선 고양이 책 손님 벤 다이어그램을 다음과 같이 그린다.
1. 어떤 변호사는 야근이 많다.
2. 모든 변호사는 야근이 많다.
3. 모든 변호사는 야근이 많지 않다.
4. 야근이 많은 어떤 사람은 변호사이다.
5. 야근이 많지 않은 어떤 사람은 변호사가 아니다.
풀이 펼치기
우선 변호사 스릴러 야근에 관한 벤 다이어그램을 아래와 같이 그린다.
1. 상식이 풍부한 어떤 사람은 책을 즐겨 읽는다.
2. 뉴스를 매일 보지 않는 어떤 사람은 책을 즐겨 읽는다.
3. 책을 즐겨 읽는 모든 사람은 상식이 풍부하지 않다.
4. 상식이 풍부한 모든 사람은 책을 즐겨 읽는다.
5. 책을 즐겨 읽는 어떤 사람은 상식이 풍부하다.
풀이 펼치기
1. 활발한 모든 학생은 그림을 잘 그린다.
2. 활발한 모든 학생은 그림을 잘 그리지 못한다.
3. 그림을 잘 그리는 어떤 학생은 활발하다.
4. 그림을 잘 그리는 모든 학생은 활발하다.
5. 그림을 잘 그리지 못하는 어떤 학생은 활발하지 않다.
풀이 펼치기
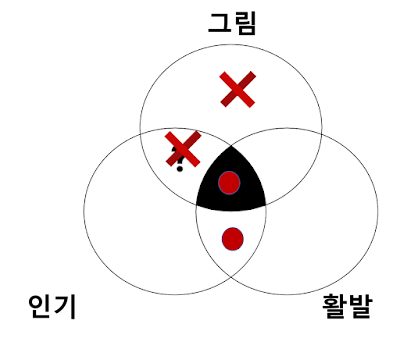
우선 벤 다이어그램을 그린다.
전제 1 : 그림을 잘 그리는 어떤 학생은 인기가 많다
임으로 어떤 부분을 ? 로 표시한다.
1. 포켓볼을 배우지 않는 어떤 사람은 탁구를 친다.
2. 탁구를 치는 모든 사람은 포켓볼을 배운다.
3. 탁구를 치는 어떤 사람은 포켓볼을 배운다.
4. 포켓볼을 배우지 않는 모든 사람은 탁구를 친다.
5. 포켓볼을 배우는 어떤 사람은 탁구를 친다.
풀이 펼치기
우선 문제에 맞게 벤 다이어그램을 그린다.































1 comment:
이런 문제를 30초안에 풀어야하다니 쉽지 않아 보이네.
Post a Comment