콤프턴 효과(Compton effect)는 입자의 파동으로의 전파 (radiation) 를 가장 직접적으로 보여주는 실험이다. 콤프턴은 주어진 파장의 범위에서 (X-Ray 파) 포일에 빛을 산란시켰는데 산란된 파장의 값이 일관되지 않는다는 것을 발견했다.
> 여기서 산란된 파장은 포일에 충돌 한 후의 빛의 파장을 의미한다. 이 파장의 값이 여러 값이 나왔다는 것이다.
> 고전역학의 개념으로는 빛은 파동이기 때문에 입자인 전자와 상호작용하지 않는다.
> 또한 파동인 빛은 입자인 전자와 에너지 교환이 될 수 없다.
>> 따라서 고전역학의 개념으로는 여러종류의 파장이 아닌 처음 입사한 그대로의 파장을 가진 빛만 나와야 한다.
콤프턴은 주어진 각으로 산란된 빛이 실제로는 두가지 구성요소로 이루어져 있다는 것을 발견했다
 |
| 가시오가피 양자역학에 나오는 그림! 처음 쏴주는 빛 ( Incident photon ) 새롭게 나온 광자 ( Scattered photon ) 광자와 충돌하여 방출된 전자 ( Recoiling electron ) |
 |
| 콤프톤 산란식을 정리하기 위해 가져온 이미지 (위키백과) |
복잡한 유도식을 생략하고 바로 우리가 알아야 할 콤프턴 산란식은 아래와 같다.
람다 프라임은 당연히 충돌 이후의 광자임으로 파장이 더 긴것!
코사인 세타에서 세타값은 광자와 전자의 충돌 각이다.
예제 1
A 100 MeV photon collides with a proton that is at rest.
What is maximum possible energy loss for the photon?
100메가 eV 의 에너지를 가진 광자가 가만히 있는 양성자와 충돌했다.
광자가 잃을 수 있는 최대의 에너지는 얼마인가?
( 단 양성자의 질량은 938 MeV/c^2 이다.)
풀이
광자가 최대로 에너지를 잃을 때는 정면으로 부딪혔을 때 이다. 광자가 완전히 뒤로 scattered(산란) 될 때 즉 위의 콤프턴 산란 식에서 cos(theta)가 -1 이 될 때 산란된 광자의 파장과 원래 파장의 길이 차이가 최대가 된다.
a. 에너지 보존
-We can find proton energy by using relativistic relation between energy and momentum.
 |
| 이해하기 쉽게 설명한 유투브 영상 |
초기 양성자의 에너지 ( 운동량이 없는 상태 , p = 0 )
:
충돌 후 양성자의 에너지 ( 이제는 운동량도 갖는 상태)
:
광자의 에너지 : hf ( h는 플랑크 상수, f는 진동수 이다.)
충돌 전과 충돌 후의 광자 양성자 에너지는 보존된다.
b. 운동량 보존
- 광자가 정지해 있는 양성자와 충돌하기 전 양성자는 운동량을 갖지 않는다.
광자는 질량을 갖지 않는다. 따라서 충돌전 광자의 운동량은 아래 별표와 같다.
- 위의 식을 통해 충돌 후 광자의 운동량은 변화된 파장의 길이 값을 곱하면 구할 수 있다는 것을 알 수 있다. ( 광자는 충돌 후에도 질량이 0이니까 )
* 광자의 p와 양자의 p가 혼용되는게 혼란을 줄 수 있을 것 같아 양자의 p를 p2로 표시했다.
:

충돌 후 양성자의 에너지 ( 이제는 운동량도 갖는 상태)
:

광자의 에너지 : hf ( h는 플랑크 상수, f는 진동수 이다.)
충돌 전과 충돌 후의 광자 양성자 에너지는 보존된다.
b. 운동량 보존
- 광자가 정지해 있는 양성자와 충돌하기 전 양성자는 운동량을 갖지 않는다.
광자는 질량을 갖지 않는다. 따라서 충돌전 광자의 운동량은 아래 별표와 같다.
- 위의 식을 통해 충돌 후 광자의 운동량은 변화된 파장의 길이 값을 곱하면 구할 수 있다는 것을 알 수 있다. ( 광자는 충돌 후에도 질량이 0이니까 )
- 충돌 후에 양성자도 운동량을 갖는다.
광자의 운동량 변화량 = 양성자의 운동량이다.
광자가 최대로 에너지를 잃을 때 임으로 광자는 양성자와 충돌 후 정반대 방향으로 운동한다.
충돌전 광자의 운동량 = 충돌 후 광자의 운동량 + 충돌 후 양자의 운동량
(여기서 충돌 후 광자의 운동 방향은 충돌전과 반대 방향임으로 운동량 크기는 - 이다)
광자의 운동량은 바로위의 식 hf/c 이다.
문제에서 주어졌듯이 광자의 초기 에너지는 100MeV 이다.
양성자가 갖는 에너지는 광자의 에너지 변화량과 같다. 따라서 양성자의 운동량은 아래와 같다.
c. 광자의 최대 에너지 손실량
a에서 구한 에너지 보존에 수치를 대입하면
b에서 구한 운동량 보존에 수치를 대입하면
위의 두식을 정리하면
따라서 초기 에너지 100MeV
최대 손실 된 후 에너지 약 82.4MeV
따라서 광자가 최대로 잃을 수 있는 에너지는 17.6MeV 이다.
예제 2
A 100keV photon collides with an electron at rest. It is scattered through 90 degree.
What is its energy after the collision? What is the kinetic energy in eV of the electron after the collision, and what is the direction of its recoil?
100keV 의 에너지를 가진 광자가 정지해 있는 전자와 충돌했다. 광자는 90도의 각도로 산란(scattered)되었다. 광자의 충돌 후 에너지는 어떻게 되는가? 전자의 반발(recoil) 방향과 그 에너지 크기는 어떻게 되는가?
단 전자의 질량은 0.510MeV/c^2 이다
광자 에너지 단위와 맞추면 510keV/c^2 이다.
광자 에너지 단위와 맞추면 510keV/c^2 이다.
충돌전 광자의 에너지 hv 는 충돌 후 광자의 에너지 hv' , 전자의 에너지 합과 같다.
b. 운동량 보존
충돌 전 광자가 x축 양의 방향으로 운동하고 있다고 하고 충돌 후 광자가 y 축 양의 방향으로 운동하고 있다고 보았다. 전자의 운동량은 x축 성분 y축 성분으로 나누어 표현하였다.
x축 방향 성분과 y축 방향 성분의 값은 일치해야 한다. 따라서
(에너지 보존 식을 이용했다)
c. 운동량 보존과 에너지 보존식 결합
a의 마지막식에 운동량 p를 대입한다.
b. 운동량 보존
충돌 전 광자가 x축 양의 방향으로 운동하고 있다고 하고 충돌 후 광자가 y 축 양의 방향으로 운동하고 있다고 보았다. 전자의 운동량은 x축 성분 y축 성분으로 나누어 표현하였다.
x축 방향 성분과 y축 방향 성분의 값은 일치해야 한다. 따라서
(에너지 보존 식을 이용했다)
c. 운동량 보존과 에너지 보존식 결합
a의 마지막식에 운동량 p를 대입한다.
x성분 운동량 y 성분 운동량을 각각 진동수에 맞게 변형하여 대입한다.
위 식을 정리하면













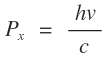




No comments:
Post a Comment